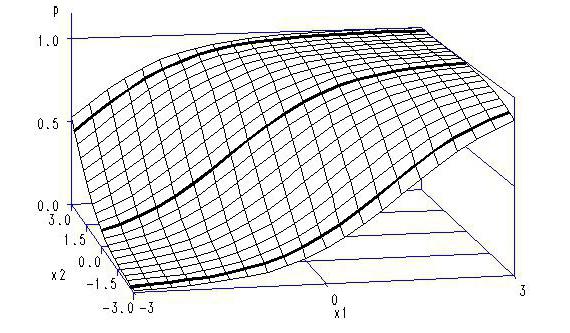
Линеарна регресија

Регресиона анализа може битистатистичке методе истраживања односа између одређених варијабли (зависне и независне). У овом случају, независне варијабле се зову "регресори", а зависни су "критеријуми". Када се врши анализа линеарне регресије, приказ зависне варијабле се изводи у облику интервалне скале. Постоји могућност не-линеарних односа између варијабли повезаних са интервалном скалом, али овај проблем је већ решен методама нелинеарне регресије, што није тема овог чланка.

Линеарна регресија се сасвим успешно користи у математичким прорачунима иу економским студијама на основу статистичких података.

Дакле, размотримо ову регресију детаљније. Са становишта математичког метода одређивања линеарне везе између неких варијабли, линеарна регресија може бити представљена у облику следеће формуле: и = а + бк. Дешифровање ове формуле може се наћи у било којем уџбенику о економетријској литератури.

Са експанзијом броја посматрања (до н пута) добијамо једноставну линеарну регресију, која је представљена формулом:

ии = А + бки + еи,

где су еи независне случајно распоређене случајне варијабле.

У овом чланку желим више пажњедати овај концепт из перспективе предвиђања будућих цијена на основу претходних података. У овој области рачунања, линеарна регресија активно користи метод најмањих квадрата, што помаже да се конструише "најпогоднија" равна линија кроз одређени низ тачака цена вриједности. Као улазни подаци користе се тачке цена, што значи максимално, минимално, затварање или отварање, као и просјечне вриједности ових вриједности (на примјер, збир максималног и минималног дијела на два). Такође, ови подаци могу бити произвољно усаглашени пре него што се изгради одговарајућа линија.

Као што је већ речено, линеарна регресијачесто се користи у аналитици како би се утврдио тренд базиран на цени и временским подацима. У том случају, нагиб регресије индикатор ће одредити величину промјена цијена по јединици времена. Један од услова за исправне одлуке, користећи овај показатељ је употреба генератора сигнала, након тренда нагиба регресије. Ако се изводи позитиван нагиб (расте линеарна регресија) купи ако показатељ вредност већа од нуле. Током негативног нагиба (смањење регресије) за продају треба да буде негативне вредности индикатора (мање од нуле).

Користећи се у одређивању најбоље линије која одговара одређеном броју тачака цена, метода најмањих квадрата укључује следећи алгоритам:

- је укупан израз квадрата разлике у цени и линије регресије;

- је однос примљене суме и броја барова у опсегу серија регресијских података;

- из добијеног резултата израчунава се квадратни корен, што одговара стандардном одступању.

Једначина парне линеарне регресије има овај модел:

и (к) = ф ^ (к),

где је и последични атрибут представљен зависном променљивом;

к је објашњавајућа или независна варијабла;

^ показује одсуство строгог функционалног односа између варијабли к и и. Према томе, у сваком појединачном случају варијабла и може бити састављена од таквих израза:

и = ик + ε,

где је и стварни резултат података;

ик - теоријски подаци резултата, одређени решавањем регресионе једначине;

ε је случајна варијабла која карактерише одступање између стварне вриједности и теоријске вриједности.