Крускалов алгоритам - конструкција оптималног скелета

У почетку 19. века геометар из Берлина, Јацоб Стеинерпоставио је задатак како повезати ова три села тако да је њихова дужина најкраћа. После тога, генерализовао је овај проблем: неопходно је пронаћи тачку на равни тако да је растојање од ње на н другим тачкама најмање. У 20. веку се наставља рад на овој теми. Било је одлучено да узмемо неколико поена и повежемо их на такав начин да је растојање између њих најкраће. Ово је све посебан случај проблема који се испитује.

Пожељни алгоритми

Крускал алгоритам се односи на "похлепе" алгоритме(такође се називају градијентом). Суштина ових - највећа победа на сваком кораку. Није увек "похлепни" алгоритми најбоље решење задатка. Постоји теорија која показује да када се примењују на одређене проблеме, они пружају оптимално рјешење. Ово је теорија матроида. Алгоритам Крускал се односи на такве проблеме.

Проналажење скелета минималне тежине

Алгоритам који се разматра конструише оптималноскелет графикона. Проблем око тога је следећи. Наредјен је неусмерјени граф без више ивица и петљи, а на његовом сету ивица дат је функција тезе в која додељује свакој ивици е број - тежину ивице - в (е). Тежина сваке подскупине скупа ивица одређује се збирима тежина његових ивица. Потребно је пронаћи скелет најмања тежина.

Опис

Крускалов алгоритам ради овако. Прво, све ивице оригиналног графа уређене су по порасту тежине. У почетку, оквир не садржи било које ивице, али укључује све вертикале графикона. Након следећег корака алгоритма, једној ивици се додаје већ изграђен део оквира, што је шума која се простире. Није одабрано произвољно. Сви ивици графа који не припадају скелету могу се назвати црвеним и зеленим. Врха сваког црвеног ребра су у једној компоненти повезаности шуме која се гради, а вертикале зелене су у различитим компонентама. Због тога, ако додате црвену ивицу, појављује се циклус, а ако је зелена - у резултујућем шумском кораку, компонента повезивања ће бити мања за један. Стога, црвену ивицу не може се додати у резултирајућу конструкцију, али било која зелена ивица може се додати да би се добила шума. Додаје се зелено ребро са минималном тежином. Као резултат, добија се скелет најмања тежина.

Имплементација

Означите тренутну шуму Ф. Подели скуп вертекса графа у повезане домене (њихове синдикалне форме Ф, а не секу се у паровима). Црвене ивице имају обе вертикале у једном делу. Део (к) је функција која враћа име дела на који к припада за сваку тачку к. Уните (к, и) је поступак који гради нову партицију која се састоји од удружења делова к и и и свих других дијелова. Нека је н број ивица графикона. Сви ови концепти укључени су у Крускалов алгоритам. Имплементација:

1. Сортирајте све ивице графикона од 1. до н-тог у растућим тежинама. (аи, би су вертикали ивице са бројем и).

2. за и = 1 до н.

3. к: = Дио (аи).

4. и: = Дио (би).

5. Ако к није једнако и онда уните (к, и), укључите ивицу и у Ф.

Тачност

Нека је Т скелет оригиналног графа конструисан коришћењем Крускаловог алгоритма, а С је његов произвољан скелет. Неопходно је доказати да в (Т) не прелази в (С).

Нека М буде скуп робова С, П бити скуп ивицаТ. Ако С није једнако Т, онда постоји ивица ет оквира Т која не припада С. Придружите се ету С. Склоњен је циклус, назовимо га Ц. Обришите било коју ивицу од Ц која припада С. Добијамо нови оквир, јер ивице, и ту је и толико врхова. Његова тежина не прелази в (С), јер в (ет) није већи од в (ес) због алгоритма Краскал. Ми ћемо поновити ову операцију (замјену ивица С за ивице Т) све док не добијемо Т. Тежина сваког каснијег добијеног оквира није већа од тежине претходне, што значи да в (Т) није већи од в (С).

Такође, исправност алгоритма Краскал следи из матроид теорема Радо-Едмонда.

Примери примене алгоритма Краскал

С обзиром на график са вертикама а, б, ц, д, е и ивицама (а,б), (а, е), (б, ц), (б, е), (ц, д), (ц, е), (д, е). Тегови ребара приказани су у табели и слици. У почетку, шума Ф у изградњи садржи све вертикале графикона и не садржи ивице. Крускалов алгоритам ће прво додати ивицу (а, е), јер има најмању тежину, а вертицес а и е су у различитим компонентама повезивања шуме Ф (ивица (а, е) је зелена), затим ивица (ц, д), јер да ова ивица има најмању тежину ивица графикона која не припада Ф, а она је зелена, а затим из истих разлога додати ивицу (а, б). Али ивица (б, е) је прескочена, иако има најмању тежину преосталих ивица, јер је црвена: вертицес б и е припадају истој повезани компоненти шуме Ф, то јест, ако додате ивицу (Ф, б) у Ф, циклус. Затим се додаје зелена ивица (б, ц), црвена ивица (ц, е) прескочи, а затим д, е. Према томе, редови (а, е), (ц, д), (а, б), (б, ц) се додају сукцесивно. Оптимални оквир почетног графа је састављен од њих. Овако функционише алгоритам у овом случају. Насликао сам. Пример овога показао.

На слици се налази граф који се састоји од две повезане компоненте. Болд линије приказују ивице оптималног оквира (зелене) конструиране помоћу алгоритма Краскал.

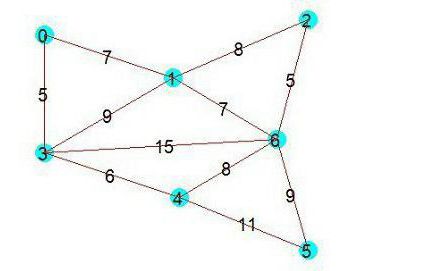
Горња слика приказује почетни графикон, а доњи показује скелет минималне тежине конструисаног за њега користећи разматран алгоритам.

Низ доданих ивица: (1,6); (0,3), (2,6) или (2,6), (0,3) - није битно; (3.4); (0.1), (1.6) или (1.6), (0.1), такође не прави разлику (5.6).

Алгоритам Краскал проналази практичну примену, на пример, за оптимизацију постављања комуникација, путева у новим стамбеним насељима у свакој земљи, али иу другим случајевима.